Lean 3 Homotopy Type Theory Library Contribution

Contributed formalized proofs regarding the notion of the 2-adjoint equivalence to the open source Homotopy Type Theory Library in Lean 3

Homotopy Type Theory (HoTT) is an intuitionistic type theory which views types as abstract, homotopy-invariant objects. As remarked in the HoTT book, this correspondence is quite remarkable as it provides a link between homotopy theory (which is related to algebraic topology, homological algebra, and higher category theory) and type theory, a field of mathematical logic and theoretical computer science. HoTT provides a type-theoretic foundation to mathematics rather then the conventional set theoretic foundation. This in turn, allows for proofs within HoTT to be formalized and understood by a computer via a proof assistant.

During the summer of 2019, myself, Daniel Carranza, and Jonathan Chang, under the supervision of Chris Kapulkin, began exploring the notion of 2-adjoint equivalences and coherences between types. This resulted in the construction, proof, and formalization of many properties one would expect from a 2-adjoint equivalence. The following summer the remaining properties were formalized by Daniel Carranza. The final, formalized proofs were added to the HoTT in Lean 3 library and can be found in the 2adj directory. Moreover, a paper describing the 2-adjoint equivalence and its formalization was published to the journal of Logical Methods in Computer Science. Additional links are provided in the publication section of this site.

Proving equality between types corresponds to showing there is a path between spaces (more specifically, that the path space is inhabited). We can also prove equality of path spaces by considering paths between paths, as we see in the first image, and equality of paths between paths by showing there is a path between paths between paths, as we see in the second image.
Table 1 is provided in section 1 of the HoTT book and provides a comparison between sets, types, logic, and homotopies.

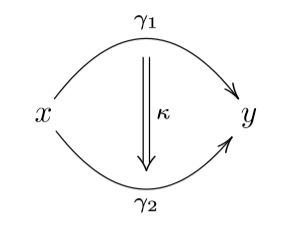
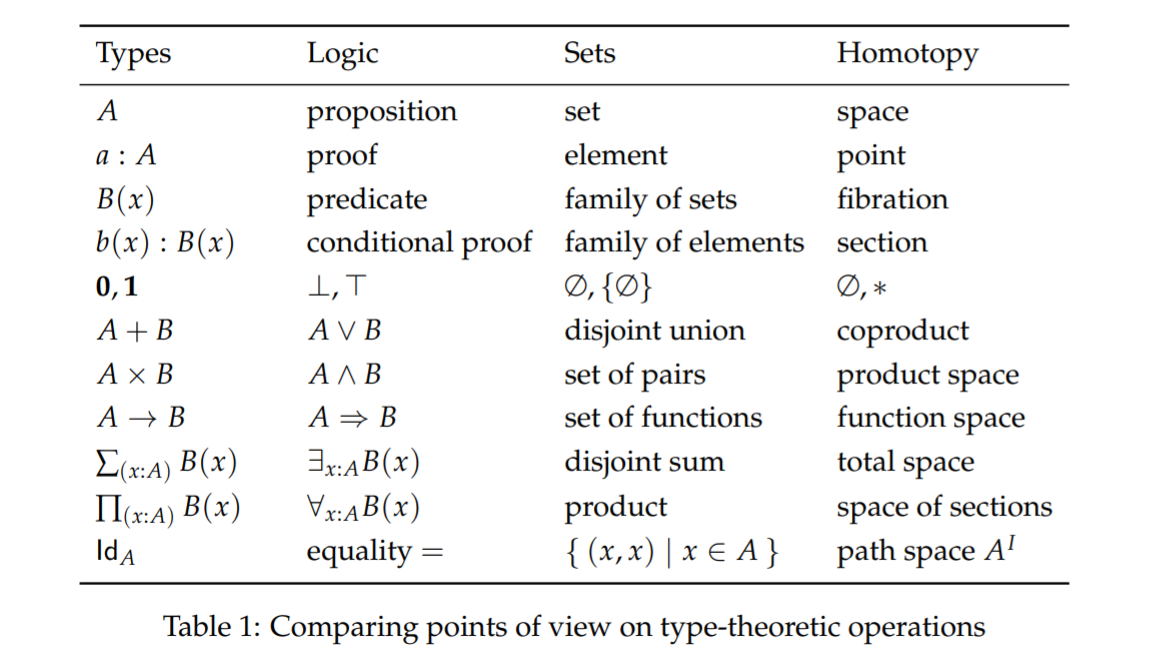
A well written and informal introduction to HoTT can be found here. The author also provides some very nice visualizations (including the thumbnail of this project).

The Homotopy Type Theory Book.

Useful Links: