Ryan Sandford | Regular Chains Library Developer

Regular chains are a powerful tool whose main application lies in solving systems of polynomial equations, inequations, and inequalities, symbolically. Loosely, regular chains are triangular systems of polynomial equations with desirable computational properties. A formal definition of a regular chain and a description of its properties and implementation in Maple can be found here.

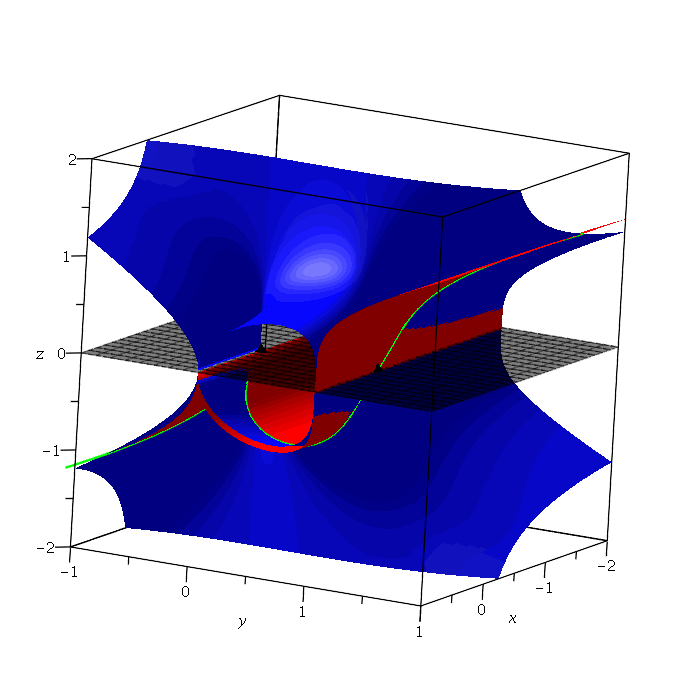
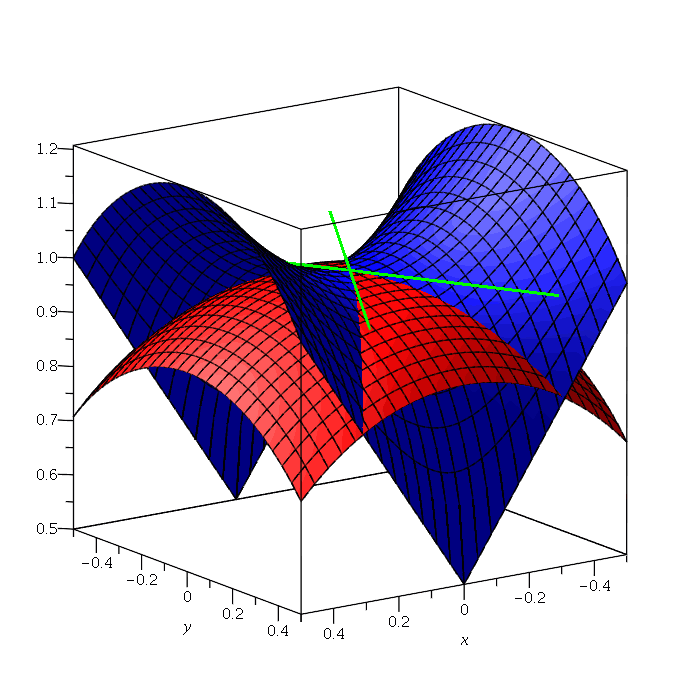
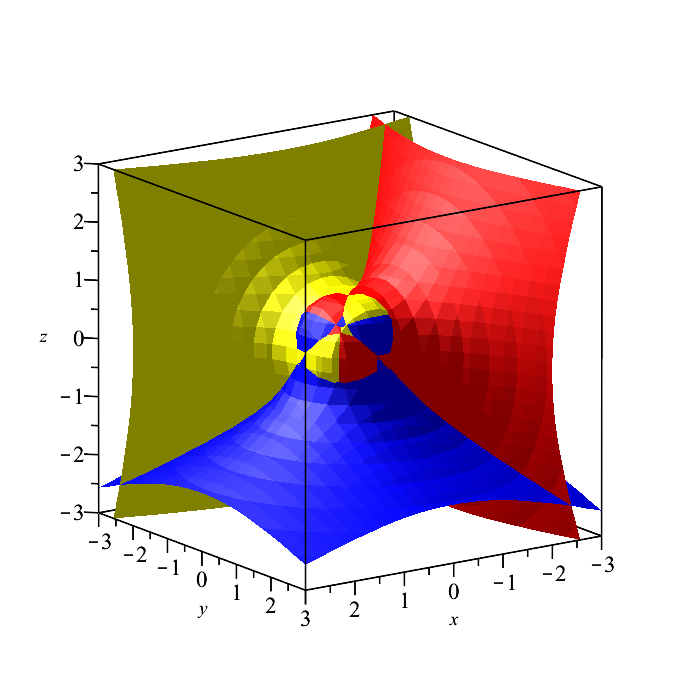
I have been developing commands in the AlgebraicGeometryTools sub-package of the RegularChains library. In particular, my work concerns the IntersectionMultiplicity, TangentCone, and TriangularizeWithMultiplicity commands, where I have introduced new, underlying algorithms and improved the implementation of previous algorithms. A paper on this work and the resulting performance improvements, is underway and will be made available shortly. For now, the corresponding slides can be found here.

The ReguarChains library is available through Maple or through the regular chains website here.

The LimitPoints command uses regular chains to compute the limit points of a space curve. Here the space curve (in green) is defined by the intersection of the red and blue surfaces, with limit points (0,0,0) and (0,1,0).

The TangentCone command uses regular chains to compute the tangent cone of a space curve. The resulting tangent cone is displayed here in green.

The TriangularizeWithMultiplicity command can be used to solve a system of polynomial equations and compute the intersection multiplicity at each solution. Above we display the polynomial system mth191, for which TriangularizeWithMultiplicity returns 8 solutions in the form of regular chains, and their corresponding intersection multiplicities.